机器学习就是让机器能自动找到一个函数（function）

• 语音识别

函数A( 语音 ）= 文字

• 图像分类

函数B( 图像 ）= 图像是什么

• 下围棋

函数C( 当前棋盘的状态 ）= 下一步落棋的位置

机器学习的类别

1、 回归（Regression）

• 输出是一个连续的数值、标量，比如PM2.5预测

2、 分类（Classification）

• 输出是一个离散的值。
• 二分类（Binary Classification）的输出就是0或1、Yes或No。
• 多分类（Multi-Category Classification）的输出就是[1,2,3,…,N]。

3、结构化学习（Structured Learnin）

• 创造性学习（黑暗大陆）

机器如何找到一个需要的函数

1、先写出一个未知参数的式子 $y=f(ax+b)$

• $a$ 与 $b$ 未知。$y=f(ax+b)$ 就是模型。
• $x$ 称为feature
• $w$ 称为weigh
• $b$ 称为bias

2、构造损失(loss)函数 $L(b,w)$

• 损失函数的输入就是模型中的 $b$ 与 $w$
• 损失函数的输出表示模型中未知参数设置的好坏

3、找到最优化（Optimizatio）的$w$与$b$

• 方法是梯度下降（Gradient Descen）
• 会有局部最优与全局最优的问题（但并不真的如此）

构造模型函数

1、更有弹性的公式模型

• 分段线段（ Linear Curve）在复杂函数表达上有局限
• 通过多个线性分段近似连续曲线
• 用S形函数（sigmoid function）代替通过多个线性分段

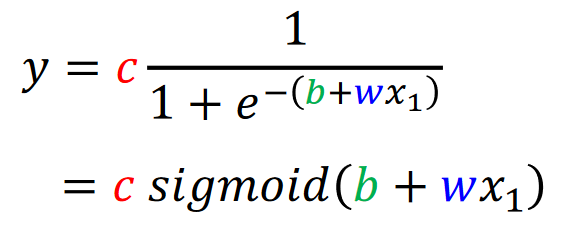
• 更改$w$,改变函数坡度
• 更改$b$,改变函数左右位置
• 更改$c$,改变函数高度

不管真实的函数是什么样的曲线，我们都可以用若干上述函数拟合逼近：

$$y=b+wx$$

改进为：

$$y=b+∑c_i sigmoid(b_i+w_ix_1)$$

当前模型就是把简单的直线，换成了若干个蓝色折线和一个常数相加。

如果用多个数据来预测：

$$y=b+∑w_ix_i$$

改进为：

$$y=b+∑_ic_isigmoid(b_i+∑_jx_jw_{ij})$$

2、公式的矩阵表示：

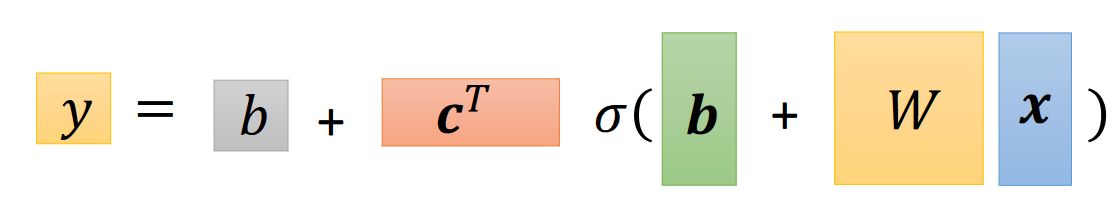
不同成分分类：

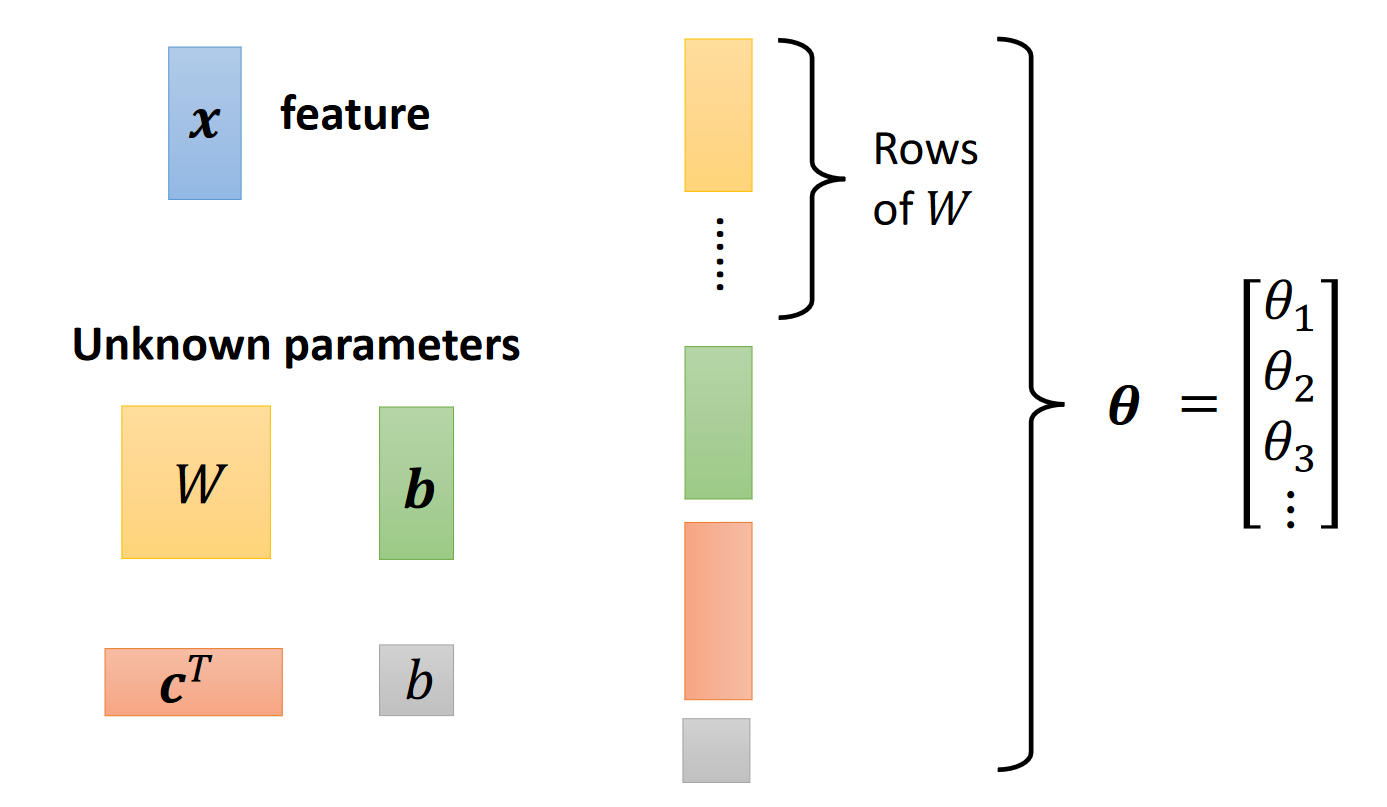
将所有未知参数统称𝜽

构造损失函数

1、定义损失函数

损失函数的定义并没有修改，仍然是之前的模式

$$L(θ)=\frac{1}{N}∑e_n$$

其中 $θ$ 表示参数向量

2、优化损失函数

1. 随机取一个初始向量 $θ^0$
2. 用 $L$ 对各参数求偏导，得到梯度向量
3. 用公式求出新的参数向量 $θ_{i + 1} = θ_i − η ∇ L ( θ^i )$；
4. 最后,梯度为零向量和已经训练足够多轮这两个条件满足其一时，结束训练，否则继续第二步。

梯度向量就是把函数对他的所有变量分别求偏导，再组合成的一个向量：

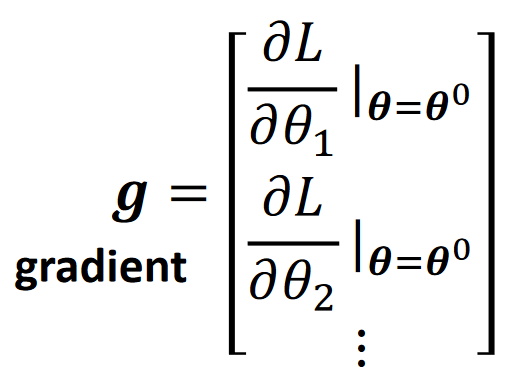
常用 $∇L$ 表示

3. 新的优化模式（Optimization of New Mode）

• L每一次迭代并不需要在所有训练数据上计算。
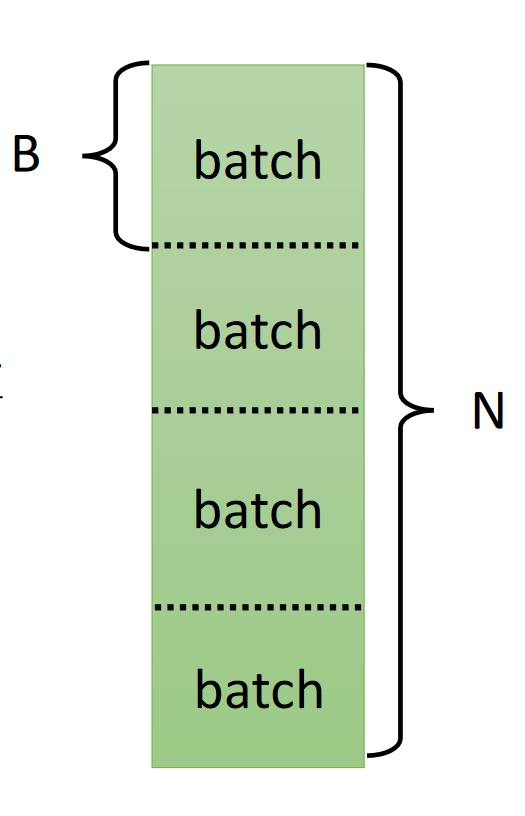
• 我们可以把训练数据分成若干份，每一份叫做一个batch。每次计算损失函数及其梯度只要在一个batch上计算即可。
• 在一个batch上计算一次叫做一次updata，在所有batch上计算一遍，则叫做一个episode。

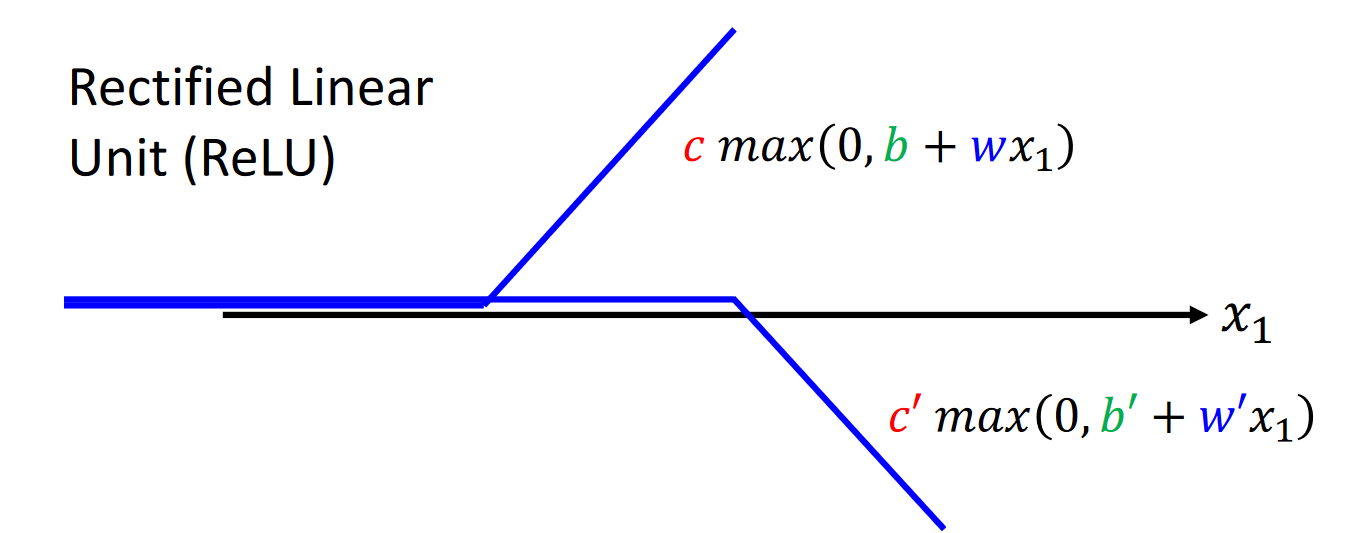
4、ReLu函数模型

ReLu（Rectified Linear Unit）函数形式如下：

$$y=cmax(0,b+w_ix)$$

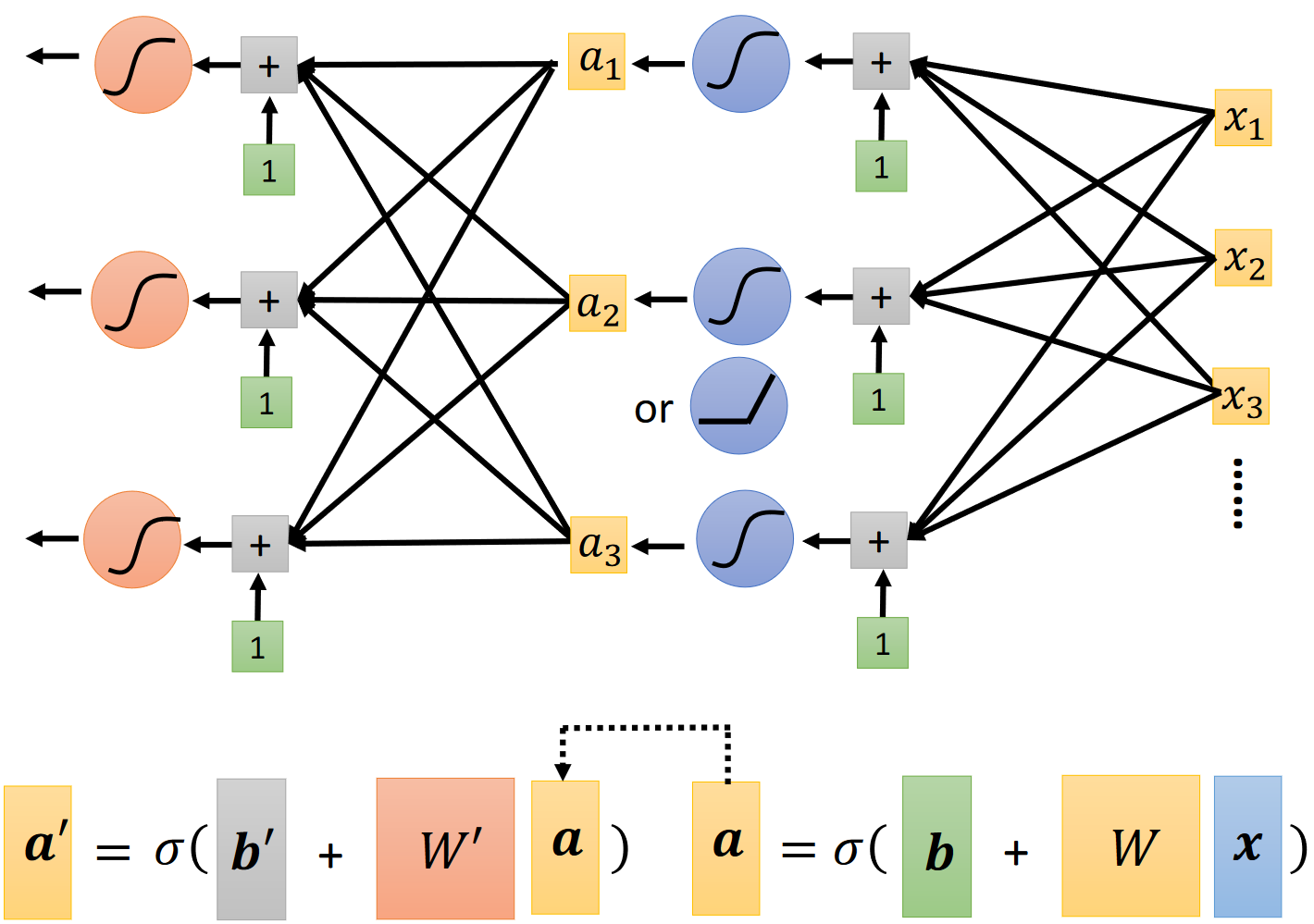
5、多层的神经网络

• 我们也可以将sigmoid函数再输入给另一个sigmoid函数以提高精度。
• 第一次将若干x输入给sigmoid函数我们可以看作第一层，再将若干sigmoid函数输入给若干sigmoid函数可以看做第二层，以此来推，我们就获得了一个多层的神经网络。

• 神经网络的层数是一个超参数。
• 每一个sigmoid函数被称作一个神经元。
• 过拟合：即模型在训练数据上过度学习，导致在测试数据上表现很差。