原文：Image Resolution Improvement Based on Sinogram Super-Resolution in PET
32nd Annual International Conference of the IEEE EMBS Buenos Aires, Argentina, August 31 - September 4, 2010
文章不是文献的完全翻译，只对主要观点与思路进行阐述。

摘要

  PET 成像的一个限制是由于预先确定的检测器宽度导致的低空间分辨率。为了克服这个限制，我们可以通过使用摆动运动来增加样本数量。由于正弦图的线扩散函数（LSF）由检测器宽度决定，然而，样本数量的增加不足以提高正弦图的分辨率。在本文中，基于从摆动运动中获得的过采样数据，我们提出了一种新颖有效的正弦图超分辨率（SR）方案。由于所提出的SR方案采用了惩罚期望最大化（EM）算法，它保证了超分辨正弦图数据的非负值。通过实验，我们证明了所提出的 SR 方案可以显着提高空间图像分辨率。

关键词——正弦图、超分辨率、正电子发射断层扫描 (PET) 和摆动。

引言

  PET 在临床环境中经常用于获取体内的代谢数据。 PET图像对于癌症的诊断和疾病程度的检查特别有用。 然而，PET 图像仍然存在空间分辨率低的问题，这是由正电子范围、非共线性和大探测器尺寸引起的。 由于此分辨率限制，很难区分图像中的少量活动。

  为了克服由于探测器尺寸而导致的空间分辨率限制，系统的许多运动机制，例如平移、半旋转、二分运动和摆动运动，被建议增加样本数量 [1]。 最广泛使用的摆动运动通过循环移动整个系统来增加样本数量。 最近，引入了摇床 [2]，而不是移动笨重的整个系统。

  尽管通过摆动运动增加了样本数量，但线扩散函数 (LSF) 不会改变，因为它由检测器尺寸决定。 因此，空间分辨率主要受 LSF 的半峰全宽 (FWHM) 的影响，而不是通过摆动运动增加的样本数量。 下图表明系统摆动运动可以在不同的系统位置提供多个正弦图集。 使用这些集合，我们可以生成采样间隔比传统系统窄的过采样正弦图。 适当地选择摆动运动，我们可以将采样间隔减少到远小于检测器宽度。 过采样数据可用于正弦图的超分辨率 (SR) [3]。

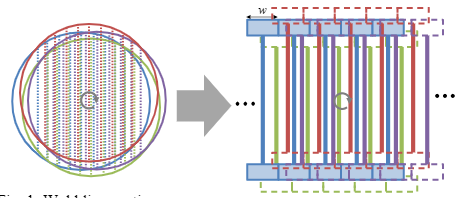
  在本文中，为了提高给定探测器尺寸的 PET 图像分辨率，我们将超分辨率方案应用于通过摆动运动过采样的正弦图。 本文组织如下。 在第二节中，我们介绍了一种超分辨率方案。 在第三节中，描述了所提出的算法。 实验结果显示在第四节中。 最后，第五节得出结论。

传统超分辨率

  SR 已在数码相机图像或视频采集中得到积极研究，以从多个低分辨率 (LR) 图像生成高分辨率 (HR) 图像。 当在完全相同的位置拍摄多个 LR 图像时，不可能从 LR 图像生成 HR 图像，因为 LR 图像之间没有任何附加信息可用。 同时，如果 LR 图像是在彼此之间具有各种子像素偏移的情况下拍摄的，则有用的信息可用于 SR。

  从 HR 图像到 LR 图像的观察模型可以描述如下：

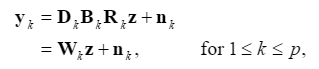
  其中 z 是 HR 图像，yk 和 nk 表示第 k 个 LR 图像及其噪声； Dk、Bk 和 Rk 分别表示下采样、模糊和变形算子。 后三项可以用单个项 Wk 代替，它表示将 HR 图像转换为第 k 个 LR 图像。 请注意，p 是 SR 的 LR 图像总数。 为了根据 (1) 中给出的观察模型获得 z，已经提出了各种迭代优化算法。

推荐的超分辨率算法

  摆动运动提供了多个正弦图集，这些正弦图集随着子检测器宽度的变化而平移。 换句话说，为每个视图获得过采样数据，并且它们的有效采样间隔可以远小于 LSF 的 FWHM。 因此，我们可以将 SR 方案应用于正弦图中每个视图的一维数据。

  如图（a）所示，如果一个正电子在 P 点湮灭，则可以使用公共立体角c 来确定探测器 A 和 B 中同时探测到两个伽马光子的概率。 基于这一观察，可以确定 LSF，如图 （b）所示。 尽管 LSF 根据与检测器的距离而变化，但为简单起见，我们假设 LSF 具有距离不变的三角形，与中心区域的形状相同。

  下图显示了当 HR 样本的检测器大小为 LR 样本的一半时，LR 样本与对应的 HR 样本之间关系的示例。

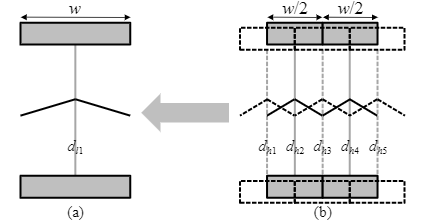
  如图所示，一个LR样本dl1的值可以写成：

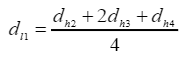
  其中 d_hi 表示 HR 样本值。 基于这种关系，我们尝试执行 1-D SR 来估计从摆动运动中获得的给定多个 LR 正弦图的 HR 正弦图。 请注意，在此 1-D SR 中，B_k 被视为 LSF。

  在迭代优化算法中，期望最大化 (EM) 算法被广泛使用，因为它保留了测量数据分布的统计特征，并且在重建图像中不提供负值 ^[4,7]。 因此，我们对正弦图的 SR 采用惩罚 EM 算法以保留上述优点 ^[6-7]。

  测得的 LR 正弦图向量 yk 可以看作服从泊松分布的随机变量，其均值为 Wkz。 然后，可以通过最大化惩罚似然函数来估计最优解向量z，即:

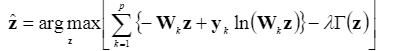
  通过使用迭代过程，z^ 可以计算如下 ^[6]：

  其中 1 是一个向量，其大小与 yk 的大小相同。 请注意，在上式中，为简单起见，假定逐个元素的向量乘法和除法，而矩阵向量乘法仍然是传统的 ^[8]。 在式（4）的迭代过程中，HR向量的初始估计0^z可以通过使用移位的多个LR向量进行线性插值得到。 然后使用乘法和除法运算更新估计的 z^。 因此，预期结果是非负的。

实验

  为了评估所提出算法的性能，我们分别进行了二维数学模拟和物理实验。

仿真实验

  为了获得正弦图数据，我们首先假设一个虚拟 PET 系统，它由一对具有旋转的平面检测器组成，如图 （a）所示。 相对检测器之间的距离设置为 400mm。 假定每个检测器宽度为 4mm。 样本数和视图数分别设置为 64 和 160。 如第 III 节所述，有限的检测器宽度会导致模糊，这可以用 LSF 表示。 为了真正反映 LSF，我们通过平均 63 x 63 行的行积分值生成每个 LR 样本值，如图 （b）所示。 其他模糊效应，例如正电子范围和非共线性，在该模拟中未被考虑。 也不考虑衰减效应以及随机和散射巧合。 因此，不需要对正弦图数据进行任何预校正。

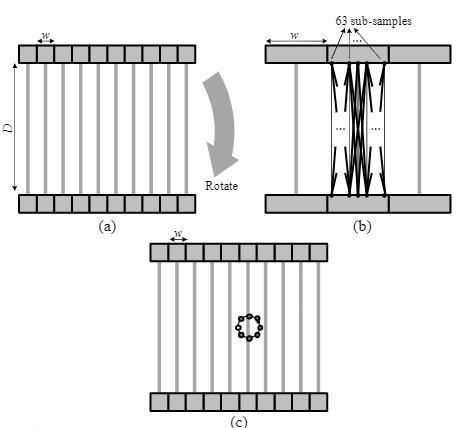
  为了模拟摆动运动，我们通过将系统的中心移动到半径为 2.5mm 的圆上均匀分布的位置来获取数据八次，如图 （c）所示。 然后我们将泊松噪声添加到获得的数据中，使重合计数总数变为 1.0M（或每个摆动点 0.125M 计数）。

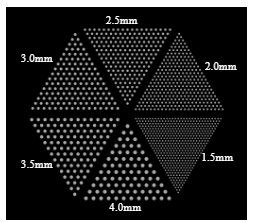
  为了进行模拟，我们采用了如下图 所示的数学 Derenzo 模型。 我们分配了大量不同直径的杆，使得相邻杆之间的中心距等于其直径的两倍。

仿真结果

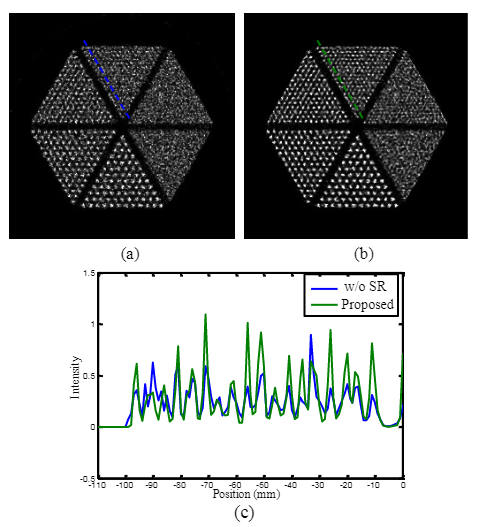
  在下图中，将获得的 HR 正弦图与通过简单内插八个 LR 正弦图获得的正弦图进行比较。 从图中可以清楚地看出，所提出的 SR 方案提高了正弦图的分辨率。 使用图中给出的正弦图。 如图 (a) 和 (b) 所示，我们基于有序子集 EM (OSEM) 算法 [5] 重建图像。 重建图像的像素网格为 256 x 256，像素尺寸为 1.0 x 1.0 mm2。

  在 OSEM 算法中，我们对 16 个子集执行 6 次迭代。 将图 （b）中给出的重建图像与图 （a）中的重建图像进行比较，我们可以看到所提出的 SR 方案显着提高了空间分辨率。 图 © 中横跨 2.5mm 直径棒的剖面也证明了所提出的 SR 方案对空间分辨率的改进。

实验验证

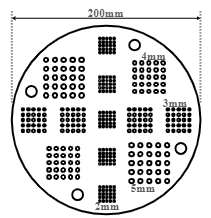
  我们还在 2D 模式下对 CTI ECAT HR+ 系统进行了物理实验。 我们使用如图 所示的分辨率体模，其直径为 200mm。 体模包含许多不同直径的棒，棒中充满浓度约为 14.1uCi/cc 的 ¹⁸F-氟脱氧葡萄糖 (¹⁸F-FDG) 溶液。

  与仿真相反，通过摆动样品而不是系统，在每个摆动点中获得八个 LR 正弦图。 在第一个摆动点获得 10 分钟的 LR 正弦图。 对于其他摆动点，考虑同位素的半衰期，增加扫描时间，使符合事件的数量与第一个正弦图相似。 对于每个 LR 正弦图，我们在应用建议的 SR 方案之前执行衰减、归一化和随机校正过程。

实验结果

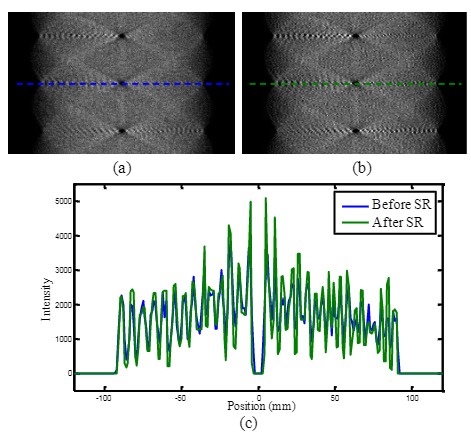
  下图将获得的 HR 正弦图与用八个 LR 正弦图插值的正弦图进行了比较。 如图 所示，可以清楚地看到所提出的 SR 方案提高了正弦图的分辨率。 使用图中给出的正弦图。 如图 (a) 和 (b) 所示，我们还基于 OSEM 算法重建图像。 重建图像的大小为 576 x 576，像素尺寸为 1.125 x 1.125 mm2。

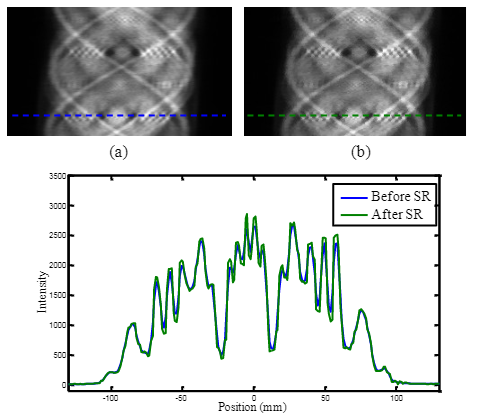
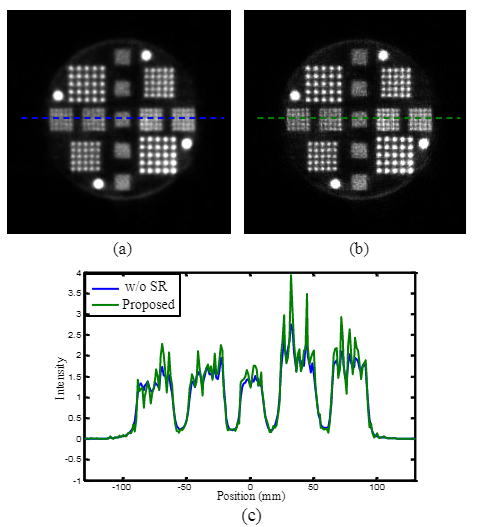
  对于基于 OSEM 的重建，我们对 16 个子集执行 6 次迭代。 将图 （b）中给出的重建图像与图 （a）中的重建图像进行比较，我们可以看到所提出的 SR 方案显着提高了空间分辨率。 图 © 中 3.0mm 直径棒的剖面图也证明了通过所提出的方案提高了空间分辨率。

结论

  在本文中，我们提出了一种新颖有效的超分辨率方案，以通过使用从系统摆动运动中获得的多个 LR 正弦图来提高图像空间分辨率。 所提出的方案基于惩罚 EM 算法，生成理想的非负 HR 正弦图。 通过实验，已经证明所提出的超分辨率方案可以显着提高图像空间分辨率。

参考文献