1. 双指针思想

代码随想录 原文

力扣题目：977.有序数组的平方

1.1 思路

暴力排序

1. 遍历每个数平方
2. 排序（时间复杂度主要取决于排序方法）$O(nlogn)$ 的时间复杂度

双指针法

• 数组是有序的
• 数组平方的最大值就在数组的两端

考虑双指针法

使用两个指针从两边到中间依次遍历找出平方最大值按顺序排列在一个新数组中。

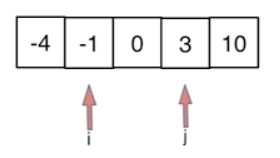
1.2 双指针法代码

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        int k = A.size() - 1;
        vector<int> result(A.size(), 0);
        //定义指针i与j，分别从两边到中间依次遍历找出**平方最大值**按顺序排列在一个新数组中
        for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j，因为最后要处理两个元素
            if (A[i] * A[i] < A[j] * A[j])  {
                result[k--] = A[j] * A[j];
                j--;
            }
            else {
                result[k--] = A[i] * A[i];
                i++;
            }
        }
        return result;
    }
};

时间复杂度为$O(n)$

2. 滑动窗口方法

代码随想录 原文

力扣题目：977.有序数组的平方

2.1 思路

暴力解法

• 两个for循环，然后不断的寻找符合条件的子序列
• 时间复杂度是 $O(n^2)$，超时

滑动窗口

使用双指针不断的调节子序列的起始位置和终止位置

滑动窗口使用主要注意：

• 窗口内是什么？
• 如何移动窗口的起始位置？
• 如何移动窗口的结束位置？

对于该题：

• 窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
• 窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。
• 窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

滑动窗口可以根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将$O(n^2)$暴力解法降为$O(n)$。

2.2 滑动窗口代码

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; //C++中常量INT_MAX和INT_MIN分别表示最大、最小整数，定义在头文件limits.h中。
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

3. 模拟行为

代码随想录 原文

力扣题目：977.有序数组的平方

3.1 思路

一定要坚持循环不变量原则（多次循环理清思路很重要）

模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

每画一条边都要坚持一致的左闭右开

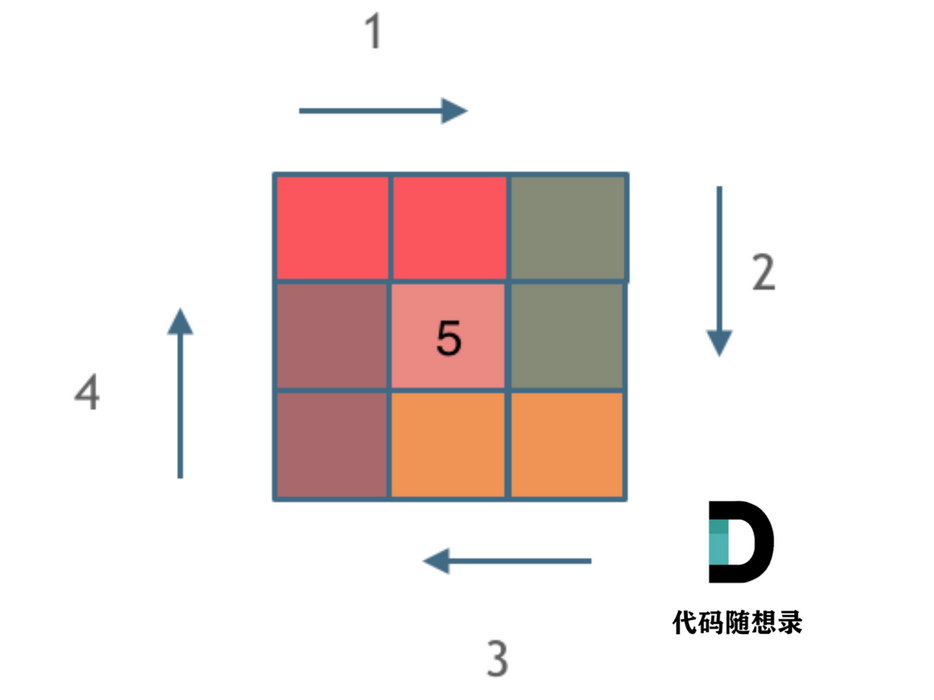
3.2 代码实现

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
        int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
        int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
        int mid = n / 2; // 矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)
        int count = 1; // 用来给矩阵中每一个空格赋值
        int offset = 1; // 需要控制每一条边遍历的长度，每次循环右边界收缩一位
        int i,j;
        while (loop --) {
            i = startx;
            j = starty;

            // 下面开始的四个for就是模拟转了一圈
            // 模拟填充上行从左到右(左闭右开)
            for (j = starty; j < n - offset; j++) {
                res[startx][j] = count++;
            }
            // 模拟填充右列从上到下(左闭右开)
            for (i = startx; i < n - offset; i++) {
                res[i][j] = count++;
            }
            // 模拟填充下行从右到左(左闭右开)
            for (; j > starty; j--) {
                res[i][j] = count++;
            }
            // 模拟填充左列从下到上(左闭右开)
            for (; i > startx; i--) {
                res[i][j] = count++;
            }

            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;

            // offset 控制每一圈里每一条边遍历的长度
            offset += 1;
        }

        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if (n % 2) {
            res[mid][mid] = count;
        }
        return res;
    }
};

• 时间复杂度 $O(n^2)$: 模拟遍历二维矩阵的时间
• 空间复杂度 $O(1)$

4. 数组总结（算法训练营第一天+第二天）

4.1 数组

• 数组是存放在连续内存空间上的相同类型数据的集合
• 删除或者增添元素的时候，必须移动其他元素的地址。
• 数组的元素是不能删的，只能覆盖。
• vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。

4.2 二分法

• 循环不变量原则：在多次循环中坚持对区间的定义，才能清楚的把握循环中的各种细节！
• 明确边界条件
• 需要能手撕

4.3 双指针法

• 双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
• 双指针时间复杂度：$O(n)$
• 在数组和链表的操作中是非常常见的

4.4 滑动窗口

• 不断调节子序列的起始位置，动态更新窗口大小
• 滑动窗口时间复杂度：$O(n)$

4.5 模拟行为

循环不变量原则：多次循环理清思路很重要

总学习时间：130min