1. 单词拆分

代码随想录：原文

力扣题目：139.单词拆分

1.1 思路

单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满

动规五部曲

1. 确定dp数组以及下标的含义

• dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词

2. 确定递推公式

• 如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）
• if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true

3. dp数组初始化

• dp[0]初始为true
• 下标非0的dp[i]初始化为false

4. 确定遍历顺序

• 先遍历 背包，再遍历物品（与物品顺序有关，排列问题）

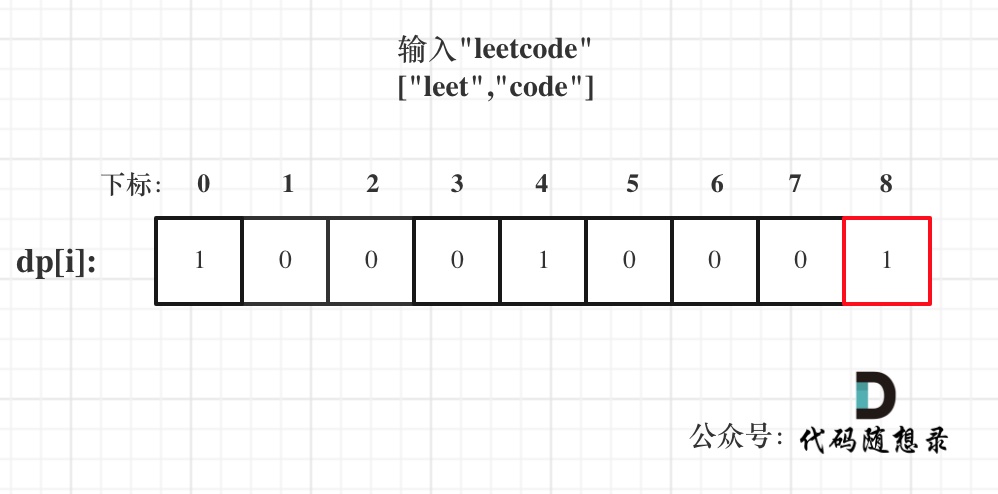
5. 举例推导dp[i]

• 以输入: s = “leetcode”, wordDict = [“leet”, “code”]为例，dp状态如图：

1.2 代码实现

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
        vector<bool> dp(s.size() + 1, false);
        dp[0] = true;
        for (int i = 1; i <= s.size(); i++) {   // 遍历背包
            for (int j = 0; j < i; j++) {       // 遍历物品
                string word = s.substr(j, i - j); //substr(起始位置，截取的个数)
                if (wordSet.find(word) != wordSet.end() && dp[j]) {
                    dp[i] = true;
                }
            }
        }
        return dp[s.size()];
    }
};

2. 多重背包理论基础

代码随想录：原文

2.1 多重背包问题

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。

2.2 解决思路

每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了

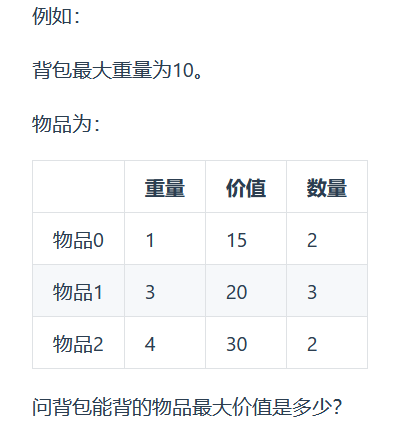
转化为：

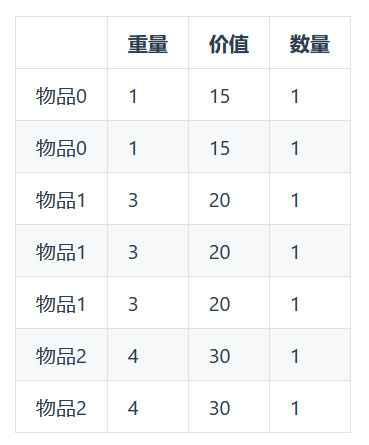
2.3 代码

void test_multi_pack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    vector<int> nums = {2, 3, 2};
    int bagWeight = 10;
    for (int i = 0; i < nums.size(); i++) {
        while (nums[i] > 1) { // nums[i]保留到1，把其他物品都展开
            weight.push_back(weight[i]);
            value.push_back(value[i]);
            nums[i]--;
        }
    }

    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
        for (int j = 0; j <= bagWeight; j++) {
            cout << dp[j] << " ";
        }
        cout << endl;
    }
    cout << dp[bagWeight] << endl;

}
int main() {
    test_multi_pack();
}

3. 背包问题总结

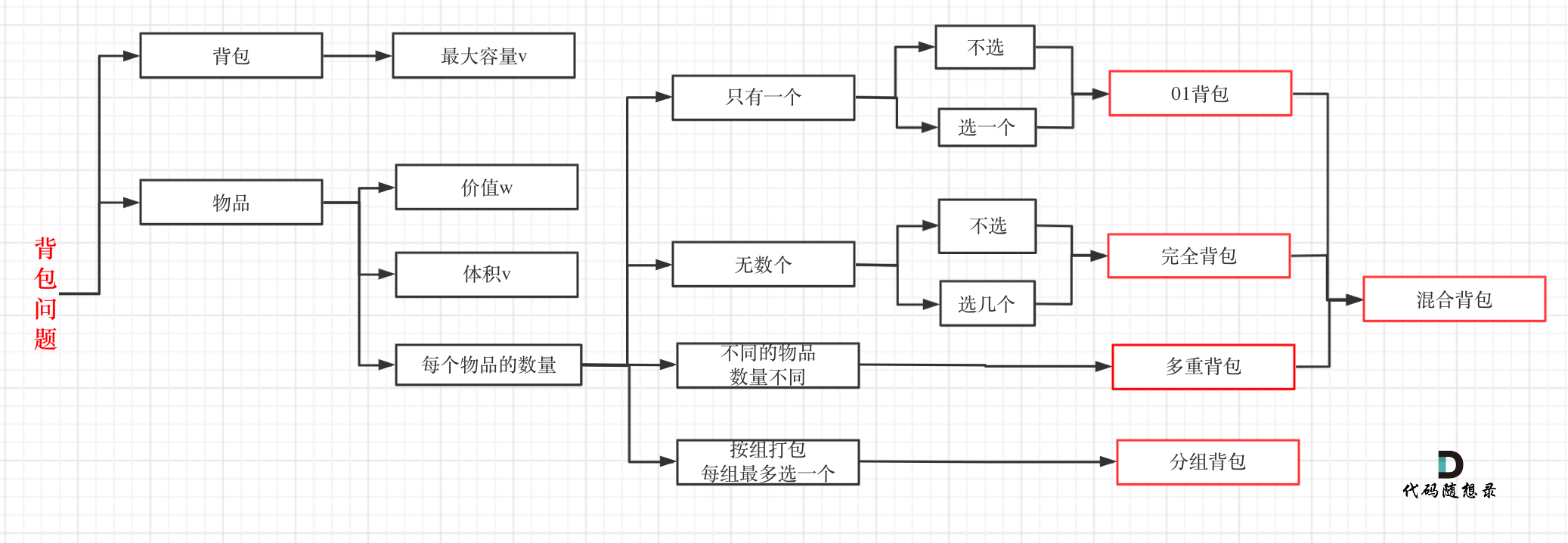
动态规划五步法：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

3.1 背包递推公式

• 问能否能装满背包（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
• 问装满背包有几种方法：dp[j] += dp[j - nums[i]]
• 问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
• 问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

3.2 遍历顺序

01背包

• 一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历

完全背包

• 如果求组合数就是外层for循环遍历物品，内层for遍历背包。
• 如果求排列数就是外层for遍历背包，内层for循环遍历物品。
• 第二层for循环是从小到大遍历