1. 组合总和

代码随想录： 原文

力扣题目： 216.组合总和III

1.1 思路

本题是要找到和为n的k个数的组合，而整个集合已经是固定的了[1,…,9]
本题k相当于树的深度，9（因为整个集合就是9个数）就是树的宽度

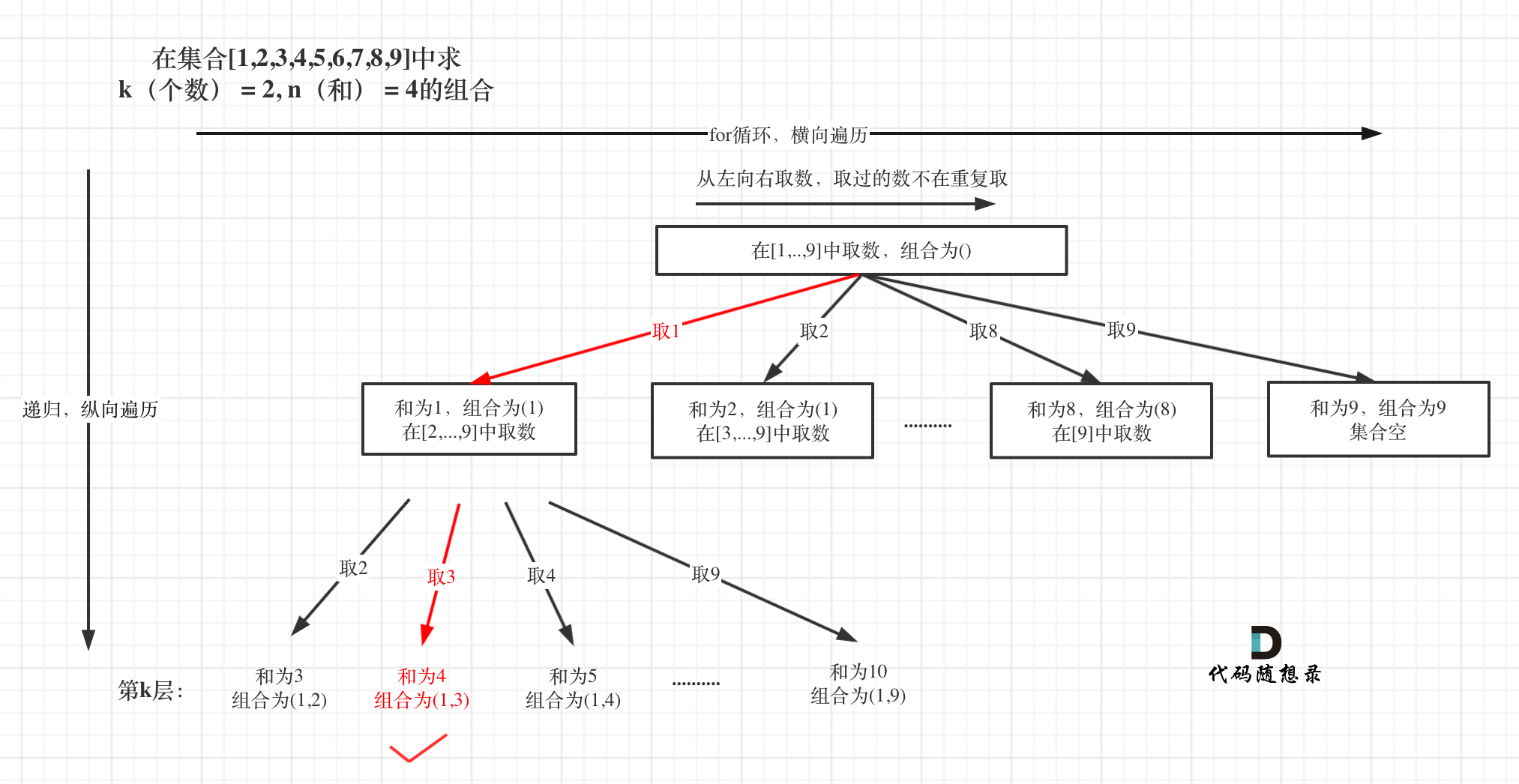
1.1.1 回溯三部曲

1. 确定递归函数参数

• 需要一维数组path来存放符合条件的结果，二维数组result来存放结果集
• 定义path 和 result为全局变量
• targetSum（int）目标和，也就是题目中的n。
• k（int）就是题目中要求k个数的集合。
• sum（int）为已经收集的元素的总和，也就是path里元素的总和。
• startIndex（int）为下一层for循环搜索的起始位置。

vector<vector<int>> result;
vector<int> path;
void backtracking(int targetSum, int k, int sum, int startIndex)

2. 确定终止条件

k其实就已经限制树的深度，因为就取k个元素，树再往下深了没有意义
path.size() 和 k相等了，就终止
如果此时path里收集到的元素和（sum） 和targetSum（就是题目描述的n）相同了，就用result收集当前的结果

if (path.size() == k) {
    if (sum == targetSum) result.push_back(path);
    return; // 如果path.size() == k 但sum != targetSum 直接返回
}

3. 单层搜索过程

• path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和

for (int i = startIndex; i <= 9; i++) {
    sum += i;
    path.push_back(i);
    backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
    sum -= i; // 回溯
    path.pop_back(); // 回溯
}

1.1.2 剪枝

• 已选元素总和如果已经大于n（图中数值为4）了，那么往后遍历就没有意义了，直接剪掉
• 剪枝的地方可以放在递归函数开始的地方，剪枝代码如下：

if (sum > targetSum) { // 剪枝操作
    return;
}

• for循环的范围也可以剪枝，i <= 9 - (k - path.size()) + 1就可以了

1.2 代码实现

class Solution {
private:
    vector<vector<int>> result; // 存放结果集
    vector<int> path; // 符合条件的结果
    // targetSum：目标和，也就是题目中的n。
    // k：题目中要求k个数的集合。
    // sum：已经收集的元素的总和，也就是path里元素的总和。
    // startIndex：下一层for循环搜索的起始位置。
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; // 如果path.size() == k 但sum != targetSum 直接返回
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i; // 处理
            path.push_back(i); // 处理
            backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
            sum -= i; // 回溯
            path.pop_back(); // 回溯
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // 可以不加
        path.clear();   // 可以不加
        backtracking(n, k, 0, 1);
        return result;
    }
};

剪枝后

class Solution {
private:
    vector<vector<int>> result; // 存放结果集
    vector<int> path; // 符合条件的结果
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (sum > targetSum) { // 剪枝操作
            return; // 如果path.size() == k 但sum != targetSum 直接返回
        }
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝
            sum += i; // 处理
            path.push_back(i); // 处理
            backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
            sum -= i; // 回溯
            path.pop_back(); // 回溯
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // 可以不加
        path.clear();   // 可以不加
        backtracking(n, k, 0, 1);
        return result;
    }
};

2. 电话号码的字母组合

代码随想录： 原文

力扣题目： 17.电话号码的字母组合

2.1 思路

1. 数字和字母如何映射
2. 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来
3. 输入1 * #按键等等异常情况

2.1.1 数字和字母如何映射

• 可以使用map或者定义一个二维数组

const string letterMap[10] = {
    "", // 0
    "", // 1
    "abc", // 2
    "def", // 3
    "ghi", // 4
    "jkl", // 5
    "mno", // 6
    "pqrs", // 7
    "tuv", // 8
    "wxyz", // 9
};

2.1.2 回溯法来解决n个for循环的问题

• 例如：输入：“23”，抽象为树形结构，如图所示：

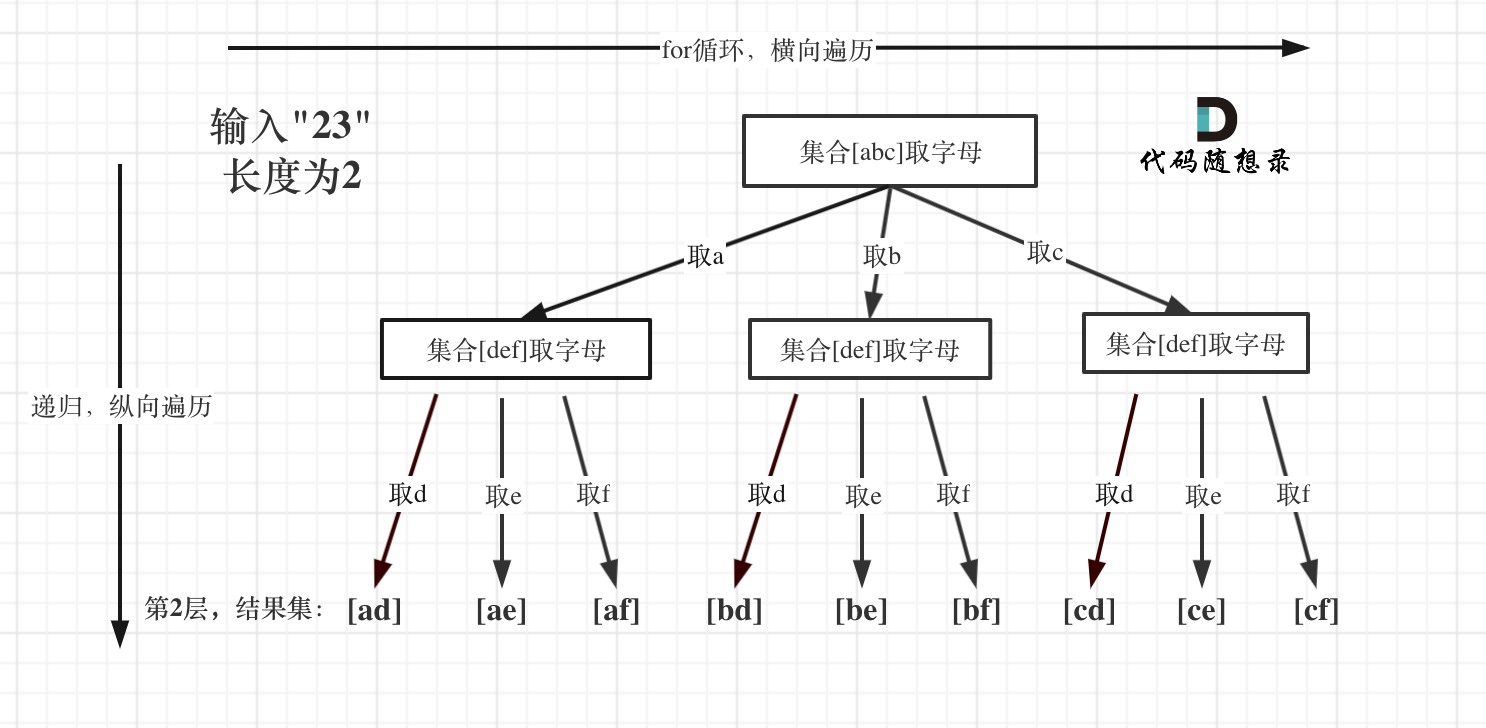
回溯三部曲：

1. 确定回溯函数参数

• 字符串s来收集叶子节点的结果
• 字符串数组result保存起来
• 参数：题目中给的string digits，然后还要有一个参数就是int型的inde
• index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度

vector<string> result;
string s;
void backtracking(const string& digits, int index)

2. 确定终止条件

• index 等于 输入的数字个数（digits.size，收集结果，结束本层递归

if (index == digits.size()) {
    result.push_back(s);
    return;
}

3. 确定单层遍历逻辑

• 要取index指向的数字，并找到对应的字符集
• for循环来处理这个字符集

int digit = digits[index] - '0';        // 将index指向的数字转为int
string letters = letterMap[digit];      // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {
    s.push_back(letters[i]);            // 处理
    backtracking(digits, index + 1);    // 递归，注意index+1，一下层要处理下一个数字了
    s.pop_back();                       // 回溯
}

注意：输入1 * #按键等等异常情况

2.2 代码实现

class Solution {
private:
    const string letterMap[10] = {
        "", // 0
        "", // 1
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz", // 9
    };
public:
    vector<string> result;
    string s;
    void backtracking(const string& digits, int index) {
        if (index == digits.size()) {
            result.push_back(s);
            return;
        }
        int digit = digits[index] - '0';        // 将index指向的数字转为int
        string letters = letterMap[digit];      // 取数字对应的字符集
        for (int i = 0; i < letters.size(); i++) {
            s.push_back(letters[i]);            // 处理
            backtracking(digits, index + 1);    // 递归，注意index+1，一下层要处理下一个数字了
            s.pop_back();                       // 回溯
        }
    }
    vector<string> letterCombinations(string digits) {
        s.clear();
        result.clear();
        if (digits.size() == 0) {
            return result;
        }
        backtracking(digits, 0);
        return result;
    }
};

3. 总结

• 别忘了处理过程 和 回溯过程是一一对应的，处理有加，回溯就要有减！

学习时间：140min