代码随想录：原文

1. 回溯法理论基础

• 回溯是递归的副产品，只要有递归就会有回溯
• 回溯法就是暴力搜索
• 回溯算法能解决如下问题：
  1. 组合问题：N个数里面按一定规则找出k个数的集合
  2. 排列问题：N个数按一定规则全排列，有几种排列方式
  3. 切割问题：一个字符串按一定规则有几种切割方式
  4. 子集问题：一个N个数的集合里有多少符合条件的子集
  5. 棋盘问题：N皇后，解数独等等

回溯三部曲

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

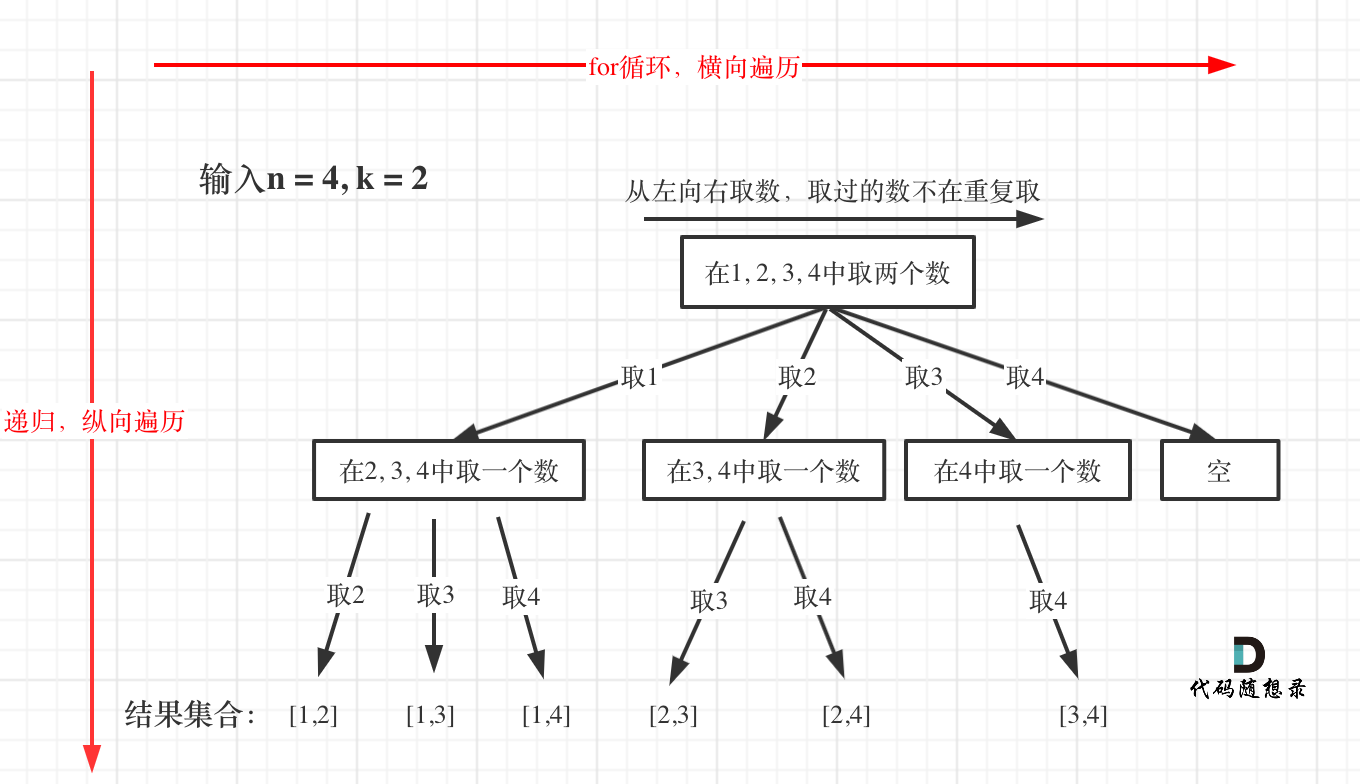
2. 组合问题

• 用递归控制for循环嵌套的数量
• for循环横向遍历，递归纵向遍历，回溯不断调整结果集

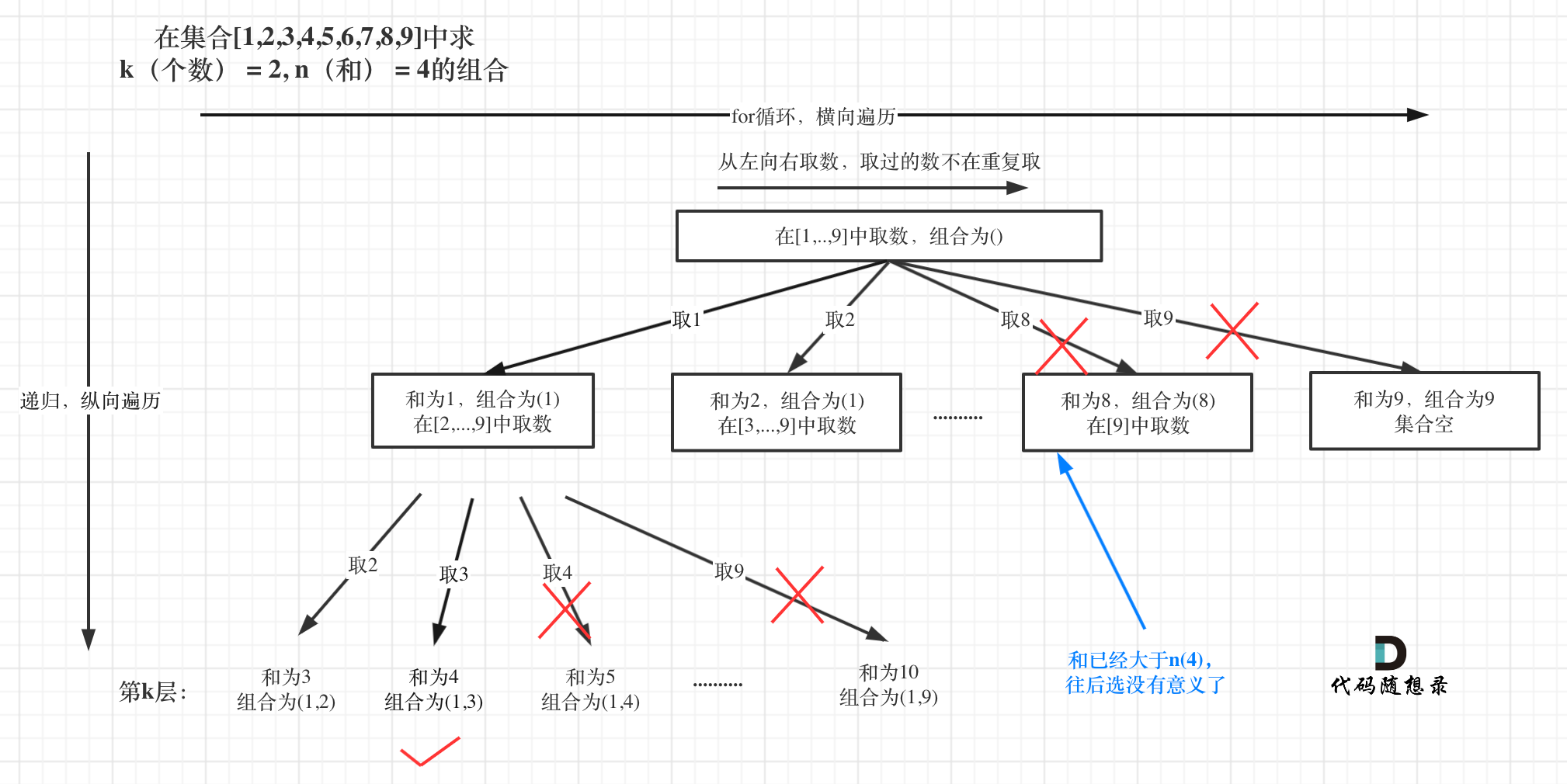
2.1 组合总和

• 求组合总和回溯算法求组合问题加了一个元素总和的限制
• 已选元素总和如果已经大于n（题中要求的和）了，那么往后遍历就没有意义了，直接剪掉

2.2 组合总和（二）

• 本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制
• 如果是一个集合来求组合的话，就需要startIndex
• 如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex

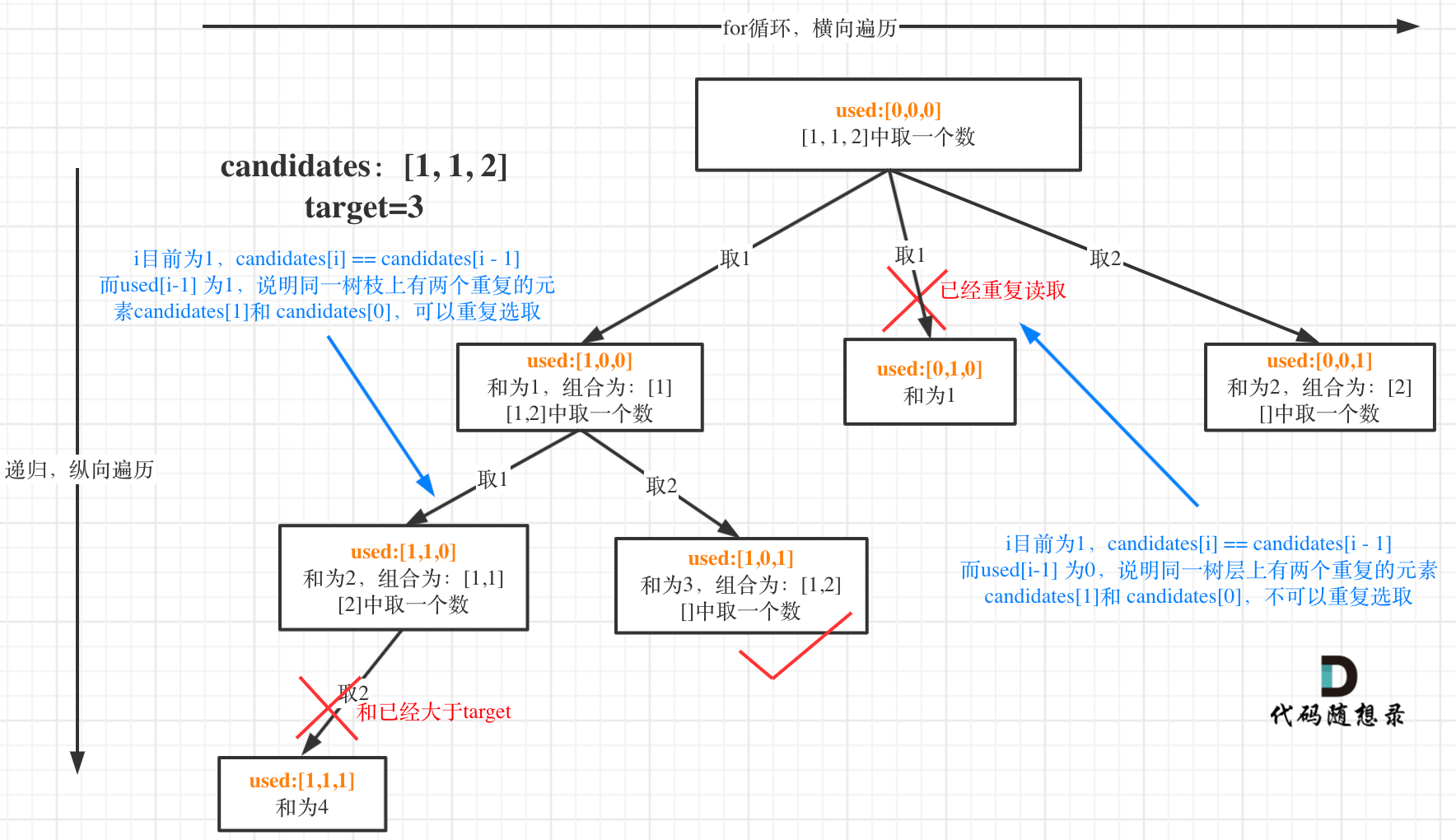
2.3 组合总和（三）

• 集合元素会有重复，但要求解集不能包含重复的组合
• 理解“树枝去重”和“树层去重”
• 可以看出在candidates[i] == candidates[i - 1]相同的情况下：
  1. used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
  2. used[i - 1] == false，说明同一树层candidates[i - 1]使用过

2.4 多个集合求组合

• 因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合

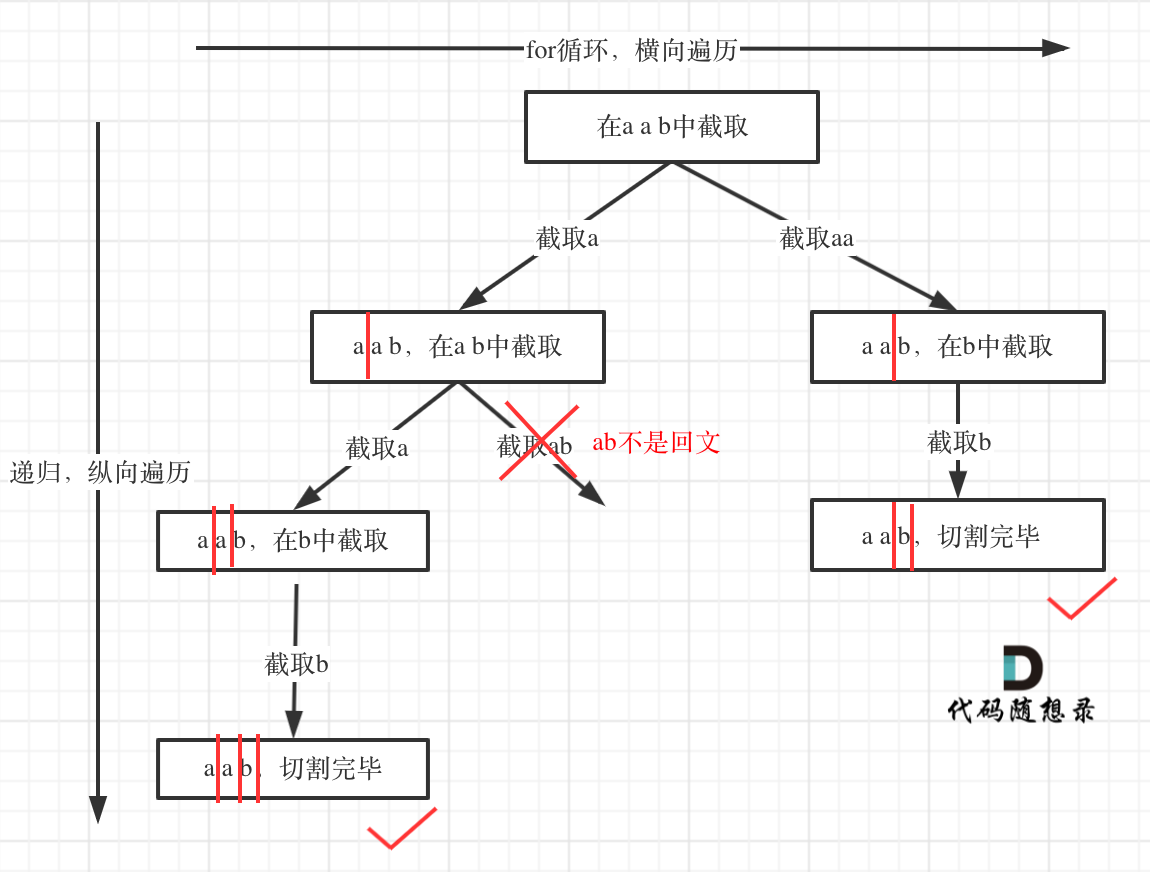
2.5 切割问题

• 切割问题用求解组合问题的思路来解决
• 需要startIndex模拟切割线

3. 子集问题

• 在树形结构中子集问题是要收集所有节点的结果，而组合问题是收集叶子节点的结果

result.push_back(path); // 收集子集，要放在终止添加的上面，否则会漏掉结果
if (startIndex >= nums.size()) { // 终止条件可以不加
    return;
}

4. 排列问题

排列问题的特点：

• 每层都是从0开始搜索而不是startIndex
• 需要used数组记录path里都放了哪些元素了
  即树层去重，效率更高